Load on tensioned ropes (rope bridge load)

Basic values

There are 5 basic values for calculating cable loads:

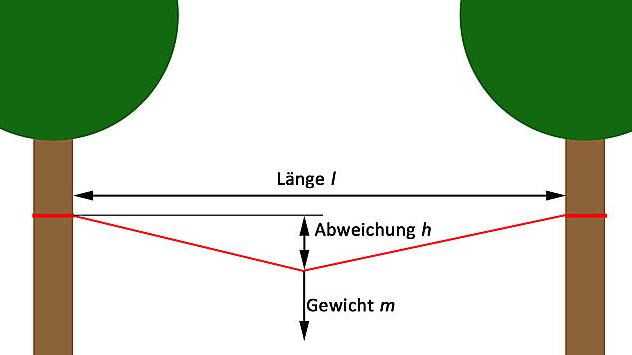
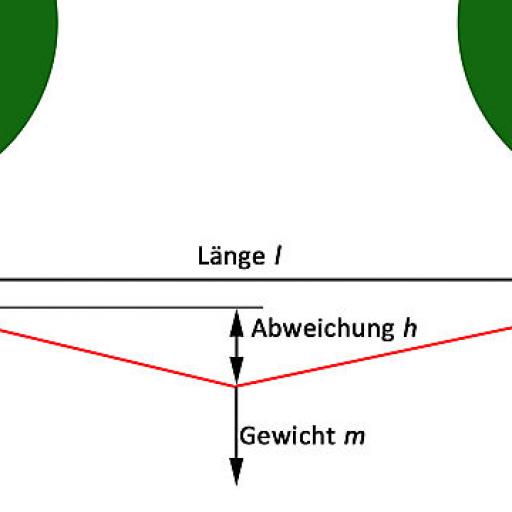
• Length l of the rope bridge. The length of the rope bridge (ideal line) in meters
• Weight m ( for mass) acting on a tensioned rope
• Deviation h Deviation from the ideal line of the rope, under load of weight m
• Tensile strength Rz of the rope. This value is given in N (Newton). With modern synthetic fiber ropes, this value can be over 35kN, but with older ropes it is significantly lower; in principle, it should be at least 24kN for rope bridges and the like.
• Tension force Fs with which a rope is tightened. This value is usually between 3 and 6kN.

The calculation is always based on the load at the center of the rope, as this is when the rope is under the greatest load.

Force in Newtons

It is important to know the unit for force, N (Newton), daN (decanewton), kN (kilonewton). The following applies:

1kN = 100daN = 1000N

These values are often mixed with weight values. The following applies:

Weight force Fg [N] = mass m [kg] * acceleration due to gravity g [m/s2]

Where g (acceleration due to gravity) is a constant 9.81m/s2 (for mental arithmetic: 10). This means that if you suspend 1kg of mass from a rope, 9.81N will act on the rope (1kg * 9.81m/s2 = 9.81N).

Neglecting

The following points are neglected when calculating rope loads:

• Dead weight of the rope

• Movement of the weight load (swing movement or falls)

In order to compensate for these points and still have reserves, we always calculate with 1/3 of the rope's tensile strength. This is particularly important for ropes that are used as a last resort (safety rope).

Basic principles

The following 3 basic principles apply:

• The more a rope sags, the lower the load
• The longer (greater distance) a rope is tensioned, the greater the load
• The tighter a rope is tensioned, the greater the load

Derivation / calculation method

The load on the rope is calculated using a trigonometric and vectorial calculation. If you do not have the appropriate basic knowledge of mathematics or physics, the derivation is difficult to understand.

This section is only for completion, it is of course not the opinion that a youth leader should be able to calculate this himself.

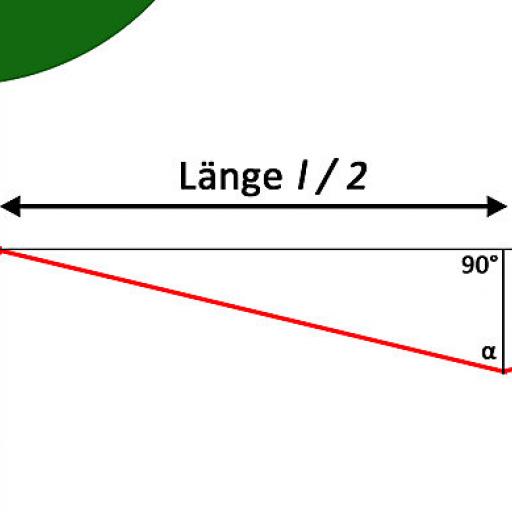
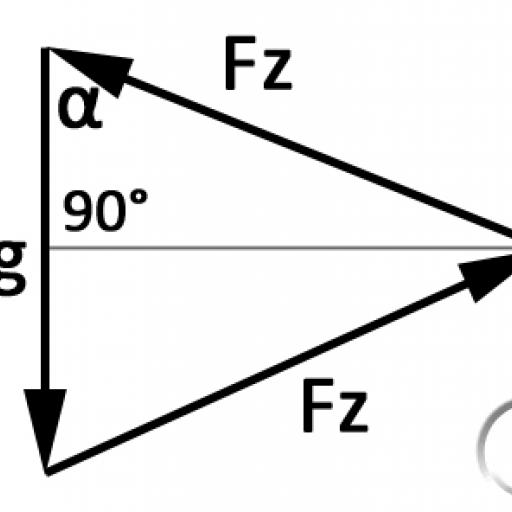
First, angle α(Fig. 1) must be defined. The following applies to α: tan α = l/(2*h) from this follows: α = tan^-1(l/(2*h))

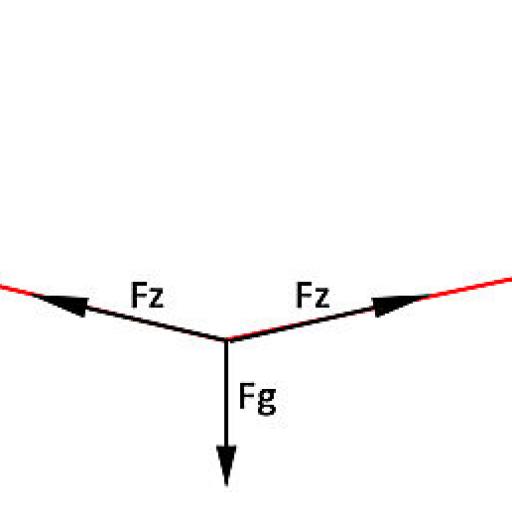
Three forces act on the center of the rope: The weight force Fg, and twice the rope tension force Fz (each in different directions, see Fig. 2). Since the structure is symmetrical, Fz is twice as great. Since the vectorial sum of all forces acting on a point is 0, the three vectors form a triangle(Fig. 3)

Fz can now be calculated relatively easily in this triangle: with the height of the triangle drawn in, the angle α (alternating angle to the previously calculated angle) and half the weight force, a trigonometric equation can again be set up: cos α = Fg/(Fz*2) from this follows: Fz = Fg/(cos α *2).

If you now use the value of the above equation for Alpha, add the tension force of the rope and multiply the whole thing by 3, you get the final required tensile strength of the rope (which is only 33% utilized):

Fo = (Fz + Fs)*3

Fo = (Fg/(cos α *2) + Fs)*3

Fo = (m*9.81/(cos(tan^-1(l/(2*h)))) *2) + Fs)*3

This equation can be transformed as desired, e.g:

m = (Fo/3 - Fs) * (cos(tan^-1(l/(2*h))) *2)/9.81

Note: The Excel formula is a little more confusing, as Excel outputs the results of trigonometric functions as radians, which must first be recalculated.

References

• Cover picture, Excel file, pictures, calculations: Provided by Jungschar Schinznach / Manuel Meier