Belasting op gespannen touwen (touwbrugbelasting)

Basiswaarden

Er zijn 5 basiswaarden voor het berekenen van kabelbelastingen:

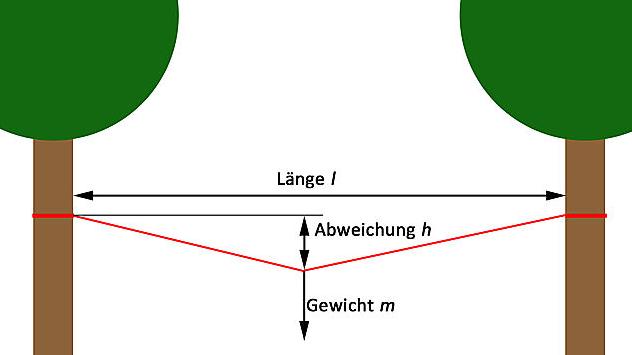
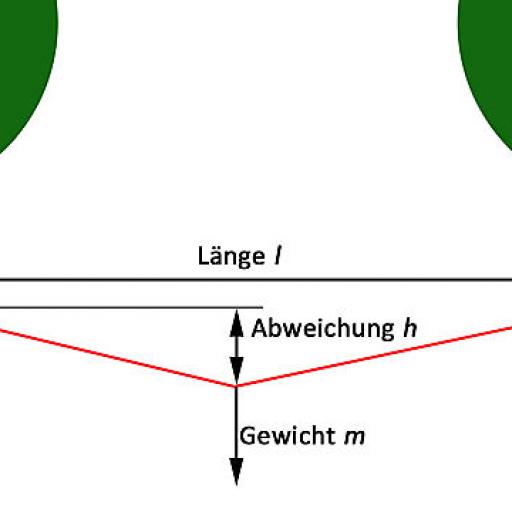
• Lengte l van de touwbrug. De lengte van de touwbrug (ideale lijn) in meters
• Gewicht m ( voor massa) dat op een gespannen touw werkt
• Afwijking h Afwijking van de ideale lijn van het touw, onder belasting van gewicht m
• Treksterkte Rz van het touw. Deze waarde wordt uitgedrukt in N (Newton). Bij moderne synthetische vezeltouwen kan deze waarde meer dan 35kN zijn, maar bij oudere touwen is ze beduidend lager. Als algemene regel moet ze minstens 24kN zijn voor touwbruggen en dergelijke.
• Spankracht Fs waarmee een touw wordt gespannen. Deze waarde ligt meestal tussen 3 en 6kN.

De berekening is altijd gebaseerd op de belasting in het midden van het touw, omdat het touw dan het zwaarst belast wordt.

Kracht in Newton

Het is belangrijk om de eenheid voor kracht te kennen, N (Newton), daN (decanewton), kN (kilonewton). Het volgende geldt:

1kN = 100daN = 1000N

Deze waarden worden vaak gemengd met gewichtswaarden. Het volgende is van toepassing:

Gewichtskracht Fg [N] = massa m [kg] * versnelling door zwaartekracht g [m/s2]

Waarbij g (versnelling door zwaartekracht) een constante is van 9,81m/s2 (voor hoofdrekenen: 10). Dit betekent dat als je 1 kg massa aan een touw hangt, er 9,81N op het touw werkt (1kg * 9,81m/s2 = 9,81N).

Verwaarlozing

De volgende punten worden verwaarloosd bij het berekenen van touwlasten:

• Dood gewicht van het touw

• Beweging van de gewichtslast (schommelbeweging of vallen)

Om deze punten te compenseren en toch reserves te hebben, rekenen we altijd met 1/3 van de treksterkte van het touw. Dit is vooral belangrijk voor touwen die als laatste redmiddel gebruikt worden (veiligheidstouw).

Basisprincipes

De volgende 3 basisprincipes zijn van toepassing:

• Hoe meer een touw doorhangt, hoe lager de belasting
• Hoe langer (grotere afstand) een touw gespannen is, hoe groter de belasting
• Hoe strakker een touw gespannen is, hoe groter de belasting

Afleiding / berekeningsmethode

De belasting op het touw wordt berekend met een goniometrische en vectoriële berekening. Als je niet over de bijbehorende basiskennis van wiskunde of natuurkunde beschikt, is de afleiding moeilijk te begrijpen.

Dit gedeelte is alleen ter aanvulling, het is natuurlijk niet de bedoeling dat een jeugdleider dit zelf kan berekenen.

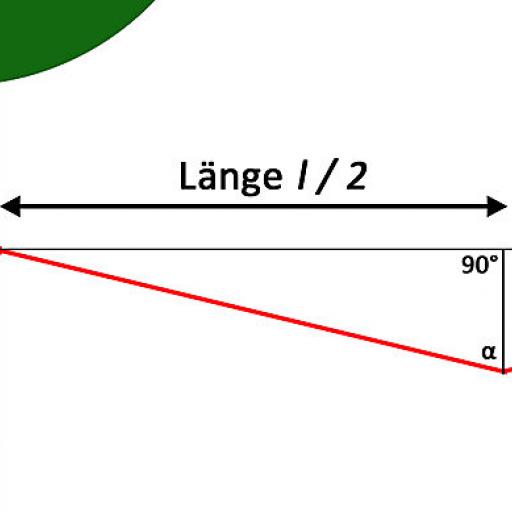
Ten eerste moet hoek α(Fig. 1) gedefinieerd worden. Voor α geldt: tan α = l/(2*h) hieruit volgt: α = tan^-1(l/(2*h))

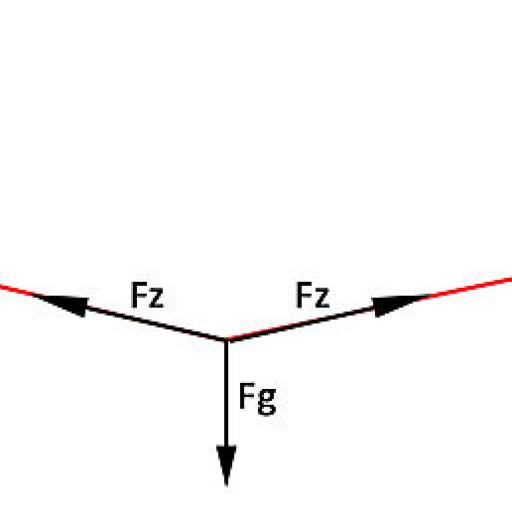
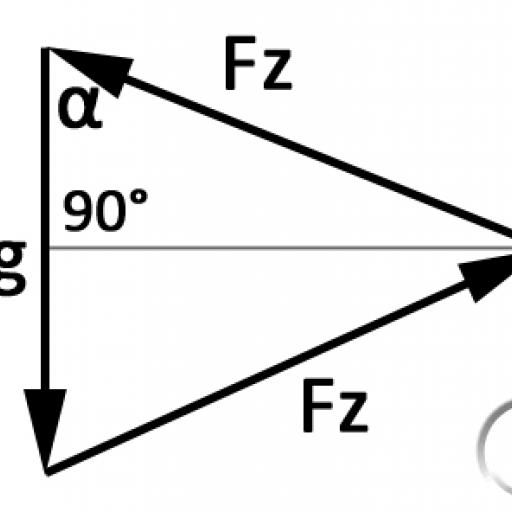
Er werken drie krachten op het midden van de kabel: De gewichtskracht Fg en tweemaal de kabelspankracht Fz (elk in verschillende richtingen, zie Fig. 2). Aangezien de constructie symmetrisch is, is Fz tweemaal dezelfde waarde. Aangezien de vectoriële som van alle krachten die op een punt inwerken 0 is, vormen de drie vectoren een driehoek(Fig. 3)

Fz kan nu relatief eenvoudig berekend worden in deze driehoek: met de hoogte van de driehoek ingetekend, de hoek α (afwisselende hoek ten opzichte van de eerder berekende hoek) en de helft van de gewichtskracht, kan opnieuw een goniometrische vergelijking opgesteld worden: cos α = Fg/(Fz*2) hieruit volgt: Fz = Fg/(cos α *2).

Als je nu de waarde van bovenstaande vergelijking gebruikt voor Alpha, de spankracht van het touw erbij optelt en het geheel vermenigvuldigt met 3, krijg je de uiteindelijke benodigde treksterkte van het touw (dat slechts voor 33% benut wordt):

Fo = (Fz + Fs)*3

Fo = (Fg/(cos α *2) + Fs)*3

Fo = (m*9,81/(cos(tan^-1(l/(2*h)))) *2) + Fs)*3

Deze vergelijking kan naar wens getransformeerd worden, bijvoorbeeld

m = (Fo/3 - Fs) * (cos(tan^-1(l/(2*h)) *2)/9.81

Opmerking: De Excel-formule is iets verwarrender, omdat Excel de resultaten van goniometrische functies uitvoert als radialen, die eerst opnieuw moeten worden berekend.

Bronvermelding

• Afbeelding omslag, Excel-bestand, afbeeldingen, berekeningen: Verstrekt door Jungschar Schinznach / Manuel Meier